おはようございます!蒼バンバンです。
今日は複利効果について、記事にしていきたいと思います。
複利効果とは?
グーグル先生に「複利効果とは?」とお聞きすると、
「複利効果とは、運用で得た利益を再び投資することで、
利益が利益を生み資産が増える効果のことです。
資産運用の場面では、投資信託の分配金など運用益を再び投資に回すことで、
利益が利益を生み、雪だるま式に資産が増えていくとされています。」
100万円を5%で20年間運用した場合
次に簡単な例をみていきましょう。
100万円を5%の利息が付く銀行に預けると、毎年5万円の利息がもらえます。
毎年利息分を引き出して、これを20年間続けると、利息だけで100万円。
5%x20年間で100%なので、元金と同額の利息がついたことになりますね、
これが単利です。
次に、同じく100万円を5%の利息が付く銀行に預けっぱなしにします。(引き出さない)
これを20年間続けるとどうなるでしょうか?
計算では、100x(1.05)^20となり、元金+利息で265万円になります。
<まとめ>100万円を5%で20年間にかけて運用した場合
・単利:200万円
計算式=100+(100x0.05)x20
・複利:265万円
計算式=100x(1.05)^20
実に65万円もの差がつきます。※実際は利息に対して税金がかかります。
1,800万円を5%で20年間運用した場合
次に新NISAの上限金額の1800万円を5%で20年間にかけて運用した場合、
・単利:3600万円
計算式=1800+(1800x0.05)x20
・複利:4775万円
計算式=1800x(1.05)^20
その差、1175万円です!これが複利の効果だと思います。
※実際は利息に対して税金がかかります。
単利と複利の違い
アインシュタインがこの「複利効果」は「人類最大の発明」と言ったそうですが、
お金を増やすためには大切な概念です。
単利と複利をグラフ化してみると、
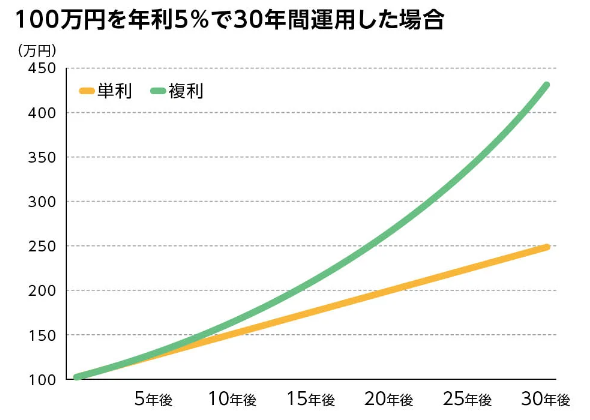
単利は一次関数(毎年一定額が増える)であるのに対して、
複利は指数関数(増える幅が年々増える)であることが一目瞭然です。
増えた利息も取り込んで、さらに雪だるま式に増えていくとよく表現されますね。
複利効果x新NISAの最強配合
蒼バンバンは、この複利効果をさらに最大限に発揮してくれるのが、
2024年から開始された新NISA制度だと考えています。
新NISAの上限1800万円を5%で20年間運用すると、
4775万円まで増える試算になります。
含み益が+2975万円まで膨れ上がりますが、
特定口座で売却した場合には、現行制度では20.315%の税金がかかります。
一方で新NISAは含み益に対して税金がかかりません。
・特定口座 :4171万円
計算式=4775ー(4775ー1800)*0.20315
・新NISA:4775万円
計算式=4775ー0(ゼロ←これが新NISA)
特定口座で運用した場合に比べて、新NISAでの税優遇は604万円!
まとめ
1800万円を年利5%で20年間運用した場合、
① 単利x特定口座 :3234万円 基準
② 複利x特定口座 :4171万円 + 937万円
③ 複利x新NISA:4775万円 +1541万円
複利効果x新NISAの絶大な威力がおわかりいただけたでしょうか。
これを夫婦2馬力でやれば当然効果も2倍です。
資産形成、ともにがんばりましょう。
それでは、また。
にほんブログ村
にほんブログ村
にほんブログ村



コメント